소수 찾기

문제정의

---

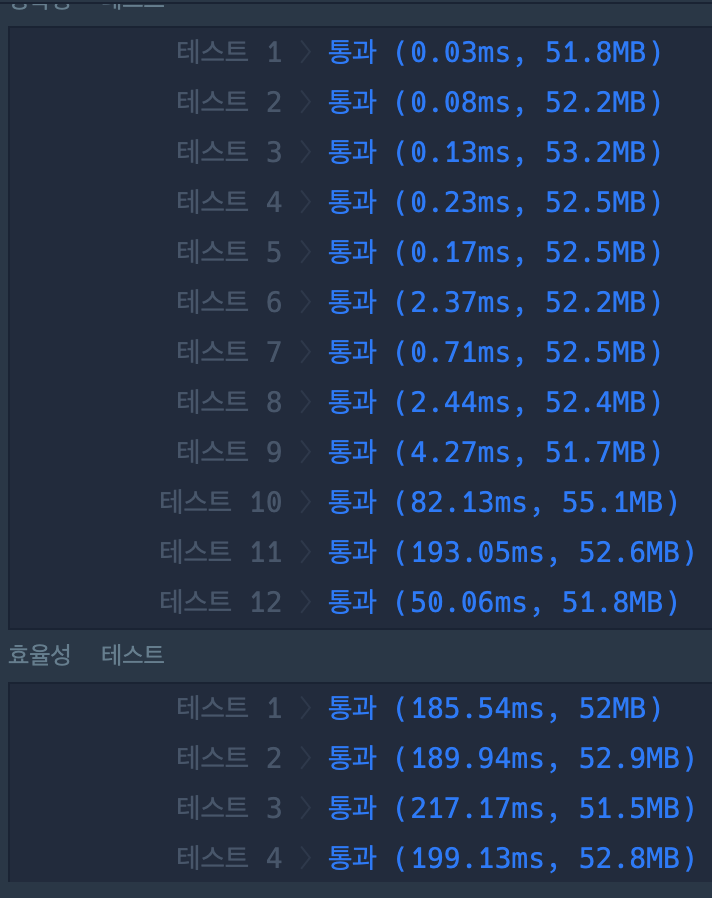
최대 자연수 값 n이 주어질 때 [1,n]에서 소수가 몇 개 있는지 출력하는 문제이다. 필자의 경우 첫번째 시도를 시간초과로 틀렸다. 그래서 질문하기를 보니 에라토테네스의 체(어떤 사람을 이걸 에라이체라고 하더라)를 활용하면 풀 수 있다고 했다. 이용했더니 한번에 풀림! 에라토테네스의 체는 큰 수가 소수가 맞는지 아닌지에 대한 판별을 할 때 유용하다고 한다. 간단히 설명을 하자면 25가 소수인지 알고 싶을 때, 2~24까지 전부 나눠보는 것이 아니라 그의 제곱근인 5를 2~5로 나눠보면 된다는 것이다. 왜 제곱근까지 나눠보면 되냐면 우리가 어떠한 수를 나눌 때 몫이 생긴다. 이 몫이 그 수의 제곱근이하이기 때문이라고 한다(더 자세히 알고 싶은 사람은 검색해보자.). 아무튼 이 원리를 이용하고 효율성 검사까지 모두 통과하였다.

문제풀이

---

전체 코드는 다음과 같다.

public class PrimeNum {
    
    public static void main(String[] args)
    {
        int n = 10;
        int answer = 0;
        boolean add = true;
        for(int i = 2; i <= n; i++)
        {
            add = true;
            for(int j = 2; j <= Math.sqrt(i); j++)
            {
                if(i%j==0)
                {
                    add = false;
                    break;
                } 
            }
            if(add)
                answer++;
                
        }
    }
}

1은 소수가 아니므로 2부터 n까지 i가 소수인지 검토하는 프로그램을 짰다. 원래 두번째 for문에서 i-1까지 나눠보는 걸로 하였는데, 에라토테네스의 체로 제곱근까지 나눠본다. 이때 등호를 넣어준 이유는 제곱근이 자연수로 딱 떨어지는 경우가 있기 때문이다. 가령 4가 소수인지 판별하기 위해선 2까지 해당하는 약수가 있는지 봐야한다. 소수판별은 위와 같이 가능하다. 소수 판별을 한다는 것을 저장하기 위해 add라는 플래그를 세워두었다. 만약 약수가 하나라도 존재하면 add는 false가 되어 answer++문을 넘어간다. 총 시간복잡도는 \(O(n\sqrt{n})\)이다.

테스트