124 나라의 숫자

Posted on Edited on In , ,

문제정의

10진법을 1,2,4에 존재하는 나라의 규칙에 따라 새로 나타내는 문제이다. 규칙을 찾아내는 것이 관건인데, 필자는 다른 사람들이랑 다른 관점으로 풀었다(코드 길이는 훨씬 길다).

문제풀이

전체 코드는 다음과 같다. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
public class Country124Num {

    //프로그래머스 문제풀이 level2 124 나라의 숫자

    public static void main(String[] args)
    {
        int n = 6;
        StringBuilder buff = new StringBuilder();
        while(n > 0)
        {
            int r = n % 3;
            n/=3;
            buff.append(String.valueOf(r));
        }
        char[] arr = buff.reverse().toString().toCharArray();
        for(int i = arr.length-1; i >= 0; i--)
        {
            if(arr[i] == '0')
            {
                int p = i;
                for(int j = i; j >=0; j--)
                {
                    if(arr[j] != '0')
                    {
                        p = j;
                        break;
                    }
                }
                if(p != i)
                {
                    for(int k = p; k < i; k++)
                    {
                        int pre_num = Integer.parseInt(String.valueOf(arr[k]));
                        char pre_char = Character.forDigit(pre_num-1, 10);
                        arr[k] = pre_char;
                        
                        int aft_num = Integer.parseInt(String.valueOf(arr[k+1]));
                        char aft_char = Character.forDigit(aft_num+3, 10);
                        arr[k+1] = aft_char;
                        
                    }
                }
            }
        }
        int start_idx = 0;
        for(int i = 0; i < arr.length; i++)
        {
            if(arr[i] != '0')
            {
                start_idx = i;
                break;
            }
                
        }
        for(int i = start_idx; i < arr.length; i++)
        {
            if(arr[i] == '3')
                arr[i] = '4';
        }
        String answer = new String(arr);
        answer = answer.substring(start_idx, arr.length);

        System.out.println(answer);
    }
    
}
부분부분 따라가보자. 
1
2
3
4
5
6
7
while(n > 0)
{
    int r = n % 3;
    n/=3;
    buff.append(String.valueOf(r));
}
char[] arr = buff.reverse().toString().toCharArray();
일단 정상적인 3진법으로 만든다. 기본적으로 이 문제는 3진법의 응용문제이다. 왜냐하면 사용하는 숫자가 총 3개이기 때문이다. 이를 대응관계로 보면 3진법의 수는 {0, 1, 2}인데, 이 문제의 경우 {4, 1, 2}로 대응된다. 그러면 3진법으로 바꿔서 4,1,2로만 바꾸면 되지 않느냐 할 수 있는데 그럴 수 없다. 3의 배수가 아닌 수는 앞서 말했던 방법이 통한다. 하지만 6을 예시로 들어보자 6의 경우 3진법으로 바꾸면 20이다. 이를 대응 관계에 비춰 바꿔보면 24이지만, 정답은 14이다. 0이 존재하지 않기 때문에 이를 처리하기 위한 방법이 필요하다. 실은 이 부분에서 꽤 고생을했는데 필자가 생각한 방법은 이렇다. 1. 3진수로 바꾼 배열을 뒤에서부터 보면서 0이 있는지 확인한다. 2. 0이 있으면 앞에서부터 빌려올 수 있는 수가 있는지 확인한다. 3. 빌려올 수 있는 수가 있다면 빌려온다. 이 때 내려받는 수는 10진법에선 10이지만, 지금은 3진법이므로 3이 되겠다. 4. 3을 빌려준 수는 1 깎인다. 5. 0을 다 없애고 나면 3인 수를 4로 바꿔준다.

이해를 돕기 위해 그림을 첨부한다.

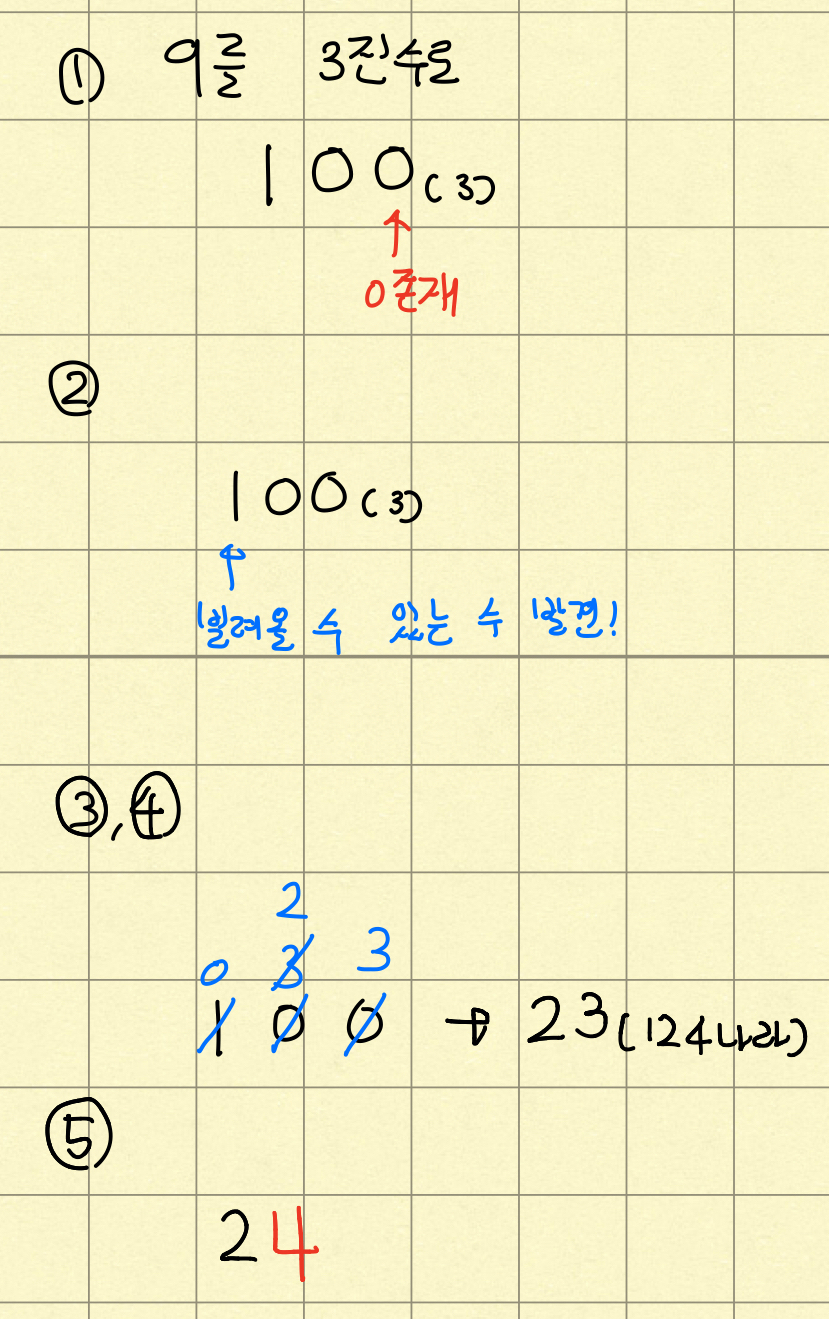
초등학생 때 했던 10진수 빼기를 생각하면 된다.

이 부분에서 시간복잡도는 3으로 나눴을 때의 자릿수만큼이므로 \(O(log3(n))\)이다.

말이 길었는데 이것만 이해하면 나머지는 코드만 읽으면 된다. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
for(int i = arr.length-1; i >= 0; i--)
{
    if(arr[i] == '0')
    {
        int p = i;
        for(int j = i; j >=0; j--)
        {
            if(arr[j] != '0')
            {
                p = j;
                break;
            }
        }
        if(p != i)
        {
            for(int k = p; k < i; k++)
            {
                int pre_num = Integer.parseInt(String.valueOf(arr[k]));
                char pre_char = Character.forDigit(pre_num-1, 10);
                arr[k] = pre_char;
                        
                int aft_num = Integer.parseInt(String.valueOf(arr[k+1]));
                char aft_char = Character.forDigit(aft_num+3, 10);
                arr[k+1] = aft_char;
                        
            }
        }
    }
}
3진수로 바꾼 수에서 뒤에서부터 보면서 0이 있는지 확인한다. 만약 0이 있다면, 자신의 앞에 있는 수에서 3을 빌릴 수 있는지 확인한다. 3을 빌릴 수 있는 숫자가 발견되면, 그 인덱스를 기억해 놨다가. 빌리고 빼는 것을 반복한다. 위 코드에서 보이는 k를 iterator로 쓰는 for문이 바로 그 부분이다(3,4번과정). 이 분의 시간 복잡도는 \(O(log3(n))\)인데, 해봤자 \(2log3(n)\)이기 때문이다. 앞쪽에서 빌리면 해당수와 앞쪽 사이에는 0이 절대로 존재할 수 없기 때문인데, 혹시 더 이해가 안간다면 이메일을 통해 언제든지 질문하기를 바란다. 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
for(int i = 0; i < arr.length; i++)
{
    if(arr[i] != '0')
    {
        start_idx = i;
        break;
    }
            
}
for(int i = start_idx; i < arr.length; i++)
{
    if(arr[i] == '3')
        arr[i] = '4';
}
거의 다왔다. 4,5과정을 거쳐도 코드적으로 해결해야하는 것이 있는데 자릿수가 있다. 아까 그림을 보면 알 수 있듯이 원래 9의 자릿수는 3자리였지만 변환 후의 자릿수는 2자릿수로 문자열을 편집해줄 필요가 있다. 앞에서 부터 0이 안나오는 인덱스를 저장해두어 나중에 substring으로 잘라준다. 그리고 3을 4로 치환한다(5번과정). 이 부분도 시간복잡도는 \(O(log3(n))\)이다.

따라서 최종 시간복잡도는 \(O(log3(n))\) 이다.

테스트



60줄을 넘었는데 다른 풀이는 고작 10줄안에 끝나서 절망했다. 하지만 할 수 있는건 계속 문제를 풀어나가는 수 밖에 없다. n에 나머지 연산을 해주고 나눌 때 3의 배수이면 -1을 해줬는데, 자릿수를 올리지 않기 위해서 그랬다고 하지만, 경험적으로 풀어봐야 이해할듯 말듯하고, 원리에 대해 명쾌하게 설명해주는 블로그가 없어서 아쉬웠다. 이 부분은 좀 더 고민해보고 이 포스트에 보충해서 쓰도록 하겠다.