다리를 지나는 트럭

문제정의

---

다리의 길이와 버틸 수 있는 최대 무게, 그리고 지나가려는 트럭의 무게가 주어진다. 트럭이 '순서대로' 다리를 건너가려고 할 때, 걸리는 최소 시간을 구하라.

문제풀이

---

전체 코드는 다음과 같다.

import java.util.*;

public class CrossBridge {

    //프로그래머스 문제풀이 level2 다리를 지나는 트럭

    public static void main(String[] args)
    {
        int bridge_length = 5;
        int weight = 5;
        int[] truck_weights = {2,2,2,2,1,1,1,1,1};
        int answer = 0;
        Queue<Integer> q = new LinkedList<>();
        int item = 0, w = 0, out = 0;
        int in_time = 1;
        while(item < truck_weights.length)
        {
            while((w+truck_weights[item] > weight) 
                    || (q.isEmpty() ? false : in_time >= q.peek()+bridge_length))
            {
                w -= truck_weights[out++];
                in_time = q.poll() + bridge_length;
            }
            q.add(in_time);
            w += truck_weights[item];

            in_time++;
            item++;
        }
        answer = --in_time + bridge_length;

        System.out.println(answer);
    }
    
}

처음에 필자는 저 순서대로를 못 읽고, 정렬을 했다가 주구장창 틀렸다. 역시 문제는 꼼꼼히 읽자. 필자는 각 트럭별로 들어오는 시간을 계산하여, 가장 마지막 시작시간에 다리의 길이를 더해주는걸로 정답을 내었다. 변수 설명을 하자면, item은 각 트럭의 id인덱스 번호이다(지금 생각해보니 truck_id가 더 나았을 것 같다.). w는 현재 다리가 버티고 있는 무게이고, out은 현재 다리를 빠져나간 트럭의 인덱스를 나타낸다. in_time은 트럭이 다리로 진입할 때의 시간이다. 이제 트럭을 큐에 넣었다 빼며, 맨 마지막으로 들어오는 트럭의 진입시간(in_time)을 계산하면 된다. 일단 while문을 넘기고 24-28번째 줄을 들여다보자. 큐에 진입하는 시간을 넣고, 다음 트럭이 오는 in_time을 계산하기 위해 item과 in_time을 1씩 증가하였다. 기본적으로 weight가 무한대라면 저것만 쓰면 될 테지만, 다리가 버틸 수 있는 무게가 있기에 while문이 필요한 것이다. while문의 첫번째 조건은 이해가 간다. 들어올 트럭의 무게를 현재 무게에 합했을 때 한계치를 넘을 경우, 앞에 있는 트럭이 빠져나가고 넣어야 한다. 뒤에 있는 조건문이 어려울 수도 있는데 이를 설명하기 위해 코드에서 쓴 테스트 케이스를 그림으로 설명하겠다.

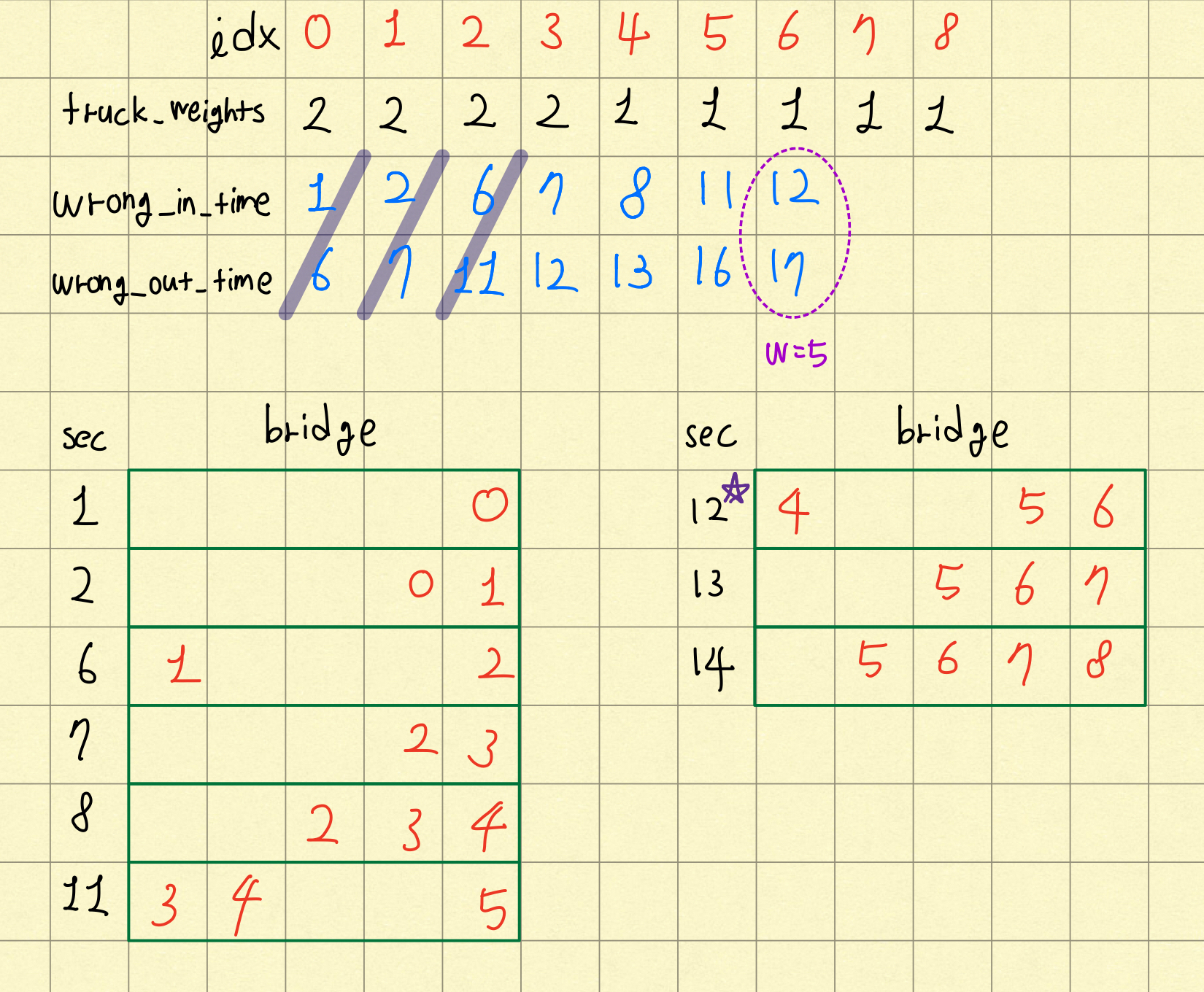
트럭의 무게들과 첫번째 조건만을 활용했을 경우 나타나는 오류를 나타낸 그림이다. 아래가 각 시간마다 다리에 있는 트럭의 위치를 나타낸 것이니 참고하면 되겠다. while문의 두번째 조건을 무시하고 첫번째 조건만을 신경쓴 채로 큐에 원소를 넣고 빼고 하다보면 idx = 6일 때 이상한 모습을 볼 수 있다. 6이 진입할 때 무게는 3이어야 하는데 5가 된 것이다. 3번 트럭이 빠지지 않은 것이 문제인데, 첫번째 조건만 가지고는 이것을 걸러낼 수 없다. 큐에서 원소를 뺄 때, 무게만 고려하는 것이 아니라 현재 in_time시간에 빠져나간 트럭들을 제거해주는 것도 같이 해야한다. 그래서 두번째 조건이 나온 것이다. 큐가 만약에 비어있다면 false를 반환하고, 아니라면 in_time에 나가야하는 트럭이 있는지 유무를 확인한 뒤, 그 원소가 큐에 남아있다면 큐에서 그 원소를 삭제한다. 모든 원소의 진입 시간이 계산되었으니, 정답을 계산한다. 마지막 반복문을 돌 때, in_time이 1 증가되었으니 이를 1줄여주고, 다리 길이를 더하면 정답이다.

이 문제의 시간복잡도를 구하기 힘들어할 수도 있는데, 어렵지 않다. 큐에 들어갔다 나오는 최대 반복을 생각하면 된다. truck_weights의 길이를 n이라 했을 때, 다 들어왔다가 다 나간다해도 2n이다. 따라서 시간복잡도는 \(O(n)\)이 된다.

테스트

이 문제같은 경우 시간을 너무 많이 소요했다. 두번째 조건을 생각하기 힘들었는데, 질문하기에서 누군가가 올려준 테스트케이스 덕분에 통과할 수 있었다.