삼각 달팽이

Posted on Edited on

문제정의

밑변과 높이의 길이가 n인 삼각형이 있고 이를 맨 위 꼭짓점에서부터 반시계방향으로 달팽이를 채우기 하고 열대로 숫자를 담아 출력하는 문제이다. 자세한 그림이 궁금한 사람은 링크를 참고해보길 바란다.

문제풀이

전체 코드는 다음과 같다. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
public class TriSnail {
    
    //프로그래머스 문제풀이 level2 삼각 달팽이

    public static void main(String[] args)
    {
        int n = 4;
        int[][] paper = new int[2*n-1][2*n-1];
        int len = n;
        int num = 1;
        int l_d_move = n%3;
        int r_move = l_d_move-1 < 0 ? 2: l_d_move-1;
        int r = 0, c = (2*n-1)/2;
        while(len != 0)
        {
            int move_id = len%3;
            if(move_id == l_d_move)
            {
                for(int i = 0; i < len; i++)
                    paper[r++][c--] = num++;
                r--;
                c++;
            }
            else if(move_id == r_move)
            {
                for(int i = 0; i < len; i++)
                {
                    c+=2;
                    paper[r][c] = num++;
                }
            }
            else
            {
                for(int i = 0; i < len; i++)
                    paper[--r][--c] = num++;
                ++r;
                --c;
            }
            len--;
        }
        int idx = 0;
        int[] answer = new int[num-1];
        for(int i = 0; i < 2*n-1; i++)
        {
            for(int j = 0; j < 2*n-1; j++)
            {
                if(paper[i][j] != 0)
                    answer[idx++] = paper[i][j];
            }
        }
    }
}
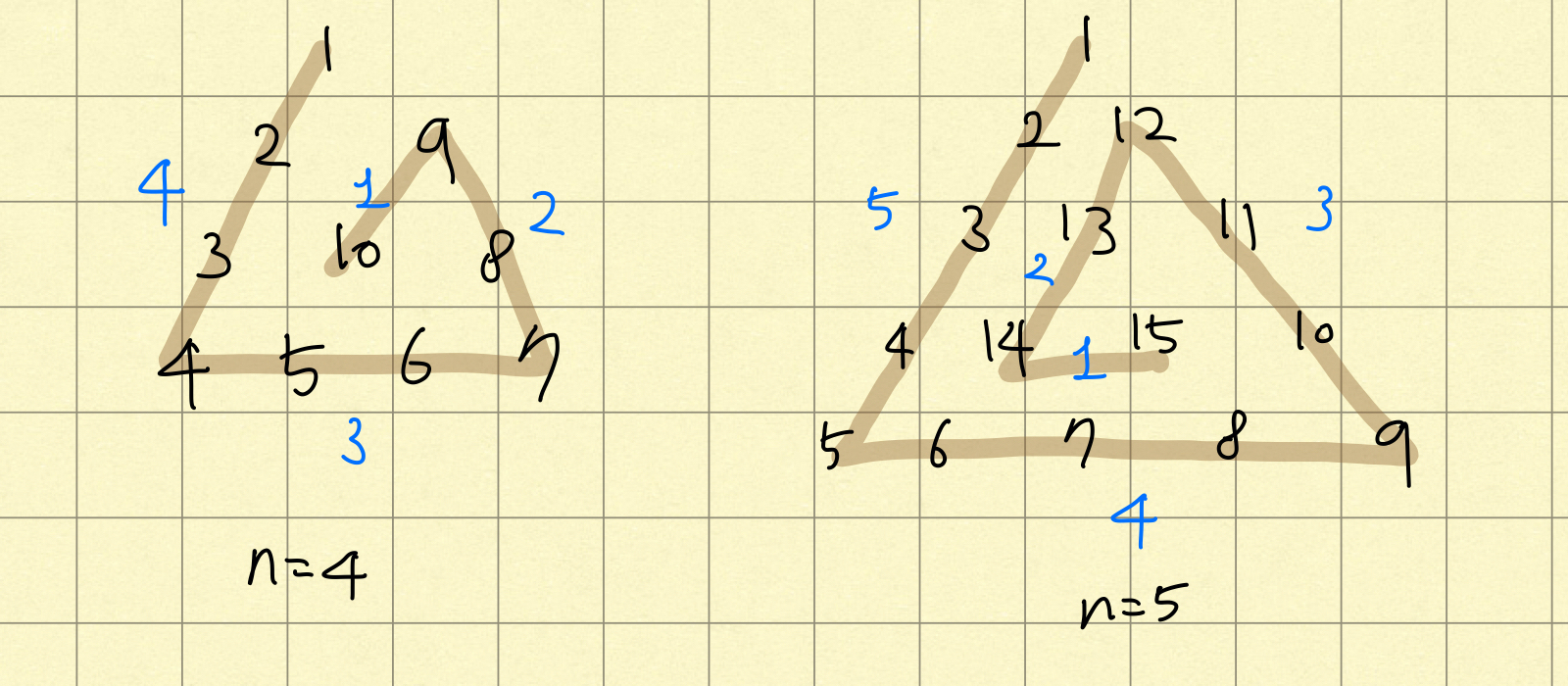
처음엔 같은 행에 속한 요소들끼리 무언가 규칙이 있을까 찾아봤지만, 너무 복잡하였다. 그래서 문제에서 주어진 달팽이를 그대로 2차원 배열에 그린 뒤, 맨 위에서부터 0이 아닌 값을 읽어들여 배열에 넣는 방법을 생각했다. 그럼 반시계 방향으로 달팽이 채우기를 하는 알고리즘이 필요한데, 이해를 돕기 위해 그림을 첨부한다.



그림을 보면 반시계 방향으로 꺽으면서 이동횟수가 1씩 감소하는 것을 볼 수 있다. 삼각형을 그리면서 움직이므로 여기서 규칙을 찾아낼 수 있다. 바로 이동횟수를 3으로 나누고 난 나머지 값을 활용해 어느 방향으로 가야하는지 알 수 있다는 것이다. n=4일 때의 달팽이 채우기를 보자, 4와 1일 때는 왼쪽 아래로 향하는 것을 볼 수 있다. n=5일 때도 보면 같은 규칙이 적용되는 것을 볼 수 있다. 5와 2는 3으로 나눈 나머지가 모두 2이므로, 2일 때 왼쪽 아래로 움직여야 하는 것을 알 수 있다.

규칙을 찾아냈으니 달팽이 채우기를 그릴 틀이 필요하다. 필자는 이것을 paper라고 선언했다. nn으로 2차원배열을 선언하고자 할텐데, 종이와 달리 배열은 중간에 낀 수가 없기 때문에 이렇게 해선 안된다. 2n-1이 길이여야 하는데 이는 아래 그림을 참고하면 왜 그런지 알 수 있다.



핵심 아이디어를 다 익혔으니 코드 세부 구현을 보자. 

1
2
3
4
5
6
7
int n = 4;
int[][] paper = new int[2*n-1][2*n-1];
        int len = n;
        int num = 1;
        int l_d_move = n%3;
        int r_move = l_d_move-1 < 0 ? 2: l_d_move-1;
        int r = 0, c = (2*n-1)/2;
왼쪽아래 움직임을 l_d_move라 표현했다. 그리고 r_move는 오른쪽으로 움직이는 경우의 나머지값을 나타낸 것이다. l_d_moved에서 1을 뺀 값이지만, 만약 l_d_move가 0인 경우, r_move는 2이기 때문에 이에 대한 처리도 함께한다. 초기 1이 위치하는 값은 (0,(2*n-1)/2)이다. 이제 달팽이 채우기로 가보자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
while(len != 0)
{
    int move_id = len%3;
    if(move_id == l_d_move)
    {
        for(int i = 0; i < len; i++)
            paper[r++][c--] = num++;
        r--;
        c++;
    }
    else if(move_id == r_move)
    {
        for(int i = 0; i < len; i++)
        {
            c+=2;
            paper[r][c] = num++;
        }
    }
    else
    {
        for(int i = 0; i < len; i++)
            paper[--r][--c] = num++;
        ++r;
        --c;
    }
    len--;
}

move_id에 따라 종이에 숫자를 채워가는 코드이다. r과 c값을 조정해나가면 된다. 범위 때문에 r이나 c값이 이상해지지 않도록 반복문 탈출 뒤 조정해주는 과정도 거친다. 여기서 필자보다 깨끗하게 코드를 짤 수 있을거라 생각하기 때문에, 이 부분에서 더 세부적인 내용은 생략한다. 여기서 시간복잡도는 \(O(n)\)이 되겠다.

1
2
3
4
5
6
7
8
9
10
int idx = 0;
int[] answer = new int[num-1];
for(int i = 0; i < n; i++)
{
    for(int j = 0; j < 2*n-1; j++)
    {
        if(paper[i][j] != 0)
            answer[idx++] = paper[i][j];
    }
}

이제 paper를 순회하면서 0이 아닌 값을 발견할 때 마다, answer에 값을 넣어주면 된다. 행은 n까지만 보면 되므로, 행의 최대값은 n으로 한다. 이 부분에서 시간복잡도는 \(O(n^2)\)이다. 따라서 최종 시간복잡도는 \(O(n^2)\)이다.

테스트



어떠한 규칙을 찾아내는 냐에 따라 코드가 천차만별인 것 같다. 코드를 좀 더 줄일 수 있는 규칙이 추가로 있는지 고민해봐야겠다.