위장

Posted on Edited on In , ,

문제정의

스파이가 위장을 하려고 한다. 옷이 종류별로 있을 때, 적어도 하나의 의상은 입고 있어야 한다. 하지만 같은 종류의 옷을 겹쳐입을 순 없다. 이 때, 스파이가 옷을 입을 수 있는 경우의 수를 구하라.

문제풀이

전체 코드는 다음과 같다. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
package level2;

import java.util.HashMap;
import java.util.Iterator;

public class Disguise {

    //프로그래머스 문제풀이 level2 위장

    public static void main(String[] args) {
        int answer = 0;
        String[][] clothes =
        {
            {"yellow_hat", "headgear"},
            {"blue_sunglasses", "eyewear"},
            {"green_turban", "headgear"}
        };
        HashMap<String, Integer> map = new HashMap<>();
        for(int i = 0; i < clothes.length; i++)
            map.put(clothes[i][1], map.getOrDefault(clothes[i][1], 0)+1);
        
        int comb_max = map.size();
        int[] clothes_num = new int[comb_max];
        
        Iterator<String> keys = map.keySet().iterator();
        int idx = 0;
        while(keys.hasNext())
        {
            String key = keys.next();
            clothes_num[idx++] = map.get(key);
            
        }
        
        int comb_cnt = 1;
        while(comb_cnt <= comb_max)
        {
            answer += getCombNum(clothes_num, comb_cnt, 1, 0);
            comb_cnt++;
        }
        System.out.println(answer);
    }
    public static int getCombNum(int[] arr, int k, int n, int idx)
    {
        if(k == 0)
            return n;
        else
        {
            int total = 0; 
            for(int i = idx; i <= arr.length-k; i++)
            {
                total += getCombNum(arr, k-1, n*arr[i], i+1);
            }
            return total;
        }
    }
}
코드가 좀 긴데 차근차근 보도록 하자. 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
HashMap<String, Integer> map = new HashMap<>();
for(int i = 0; i < clothes.length; i++)
    map.put(clothes[i][1], map.getOrDefault(clothes[i][1], 0)+1);

int comb_max = map.size();
int[] clothes_num = new int[comb_max];

Iterator<String> keys = map.keySet().iterator();
int idx = 0;
while(keys.hasNext())
{
    String key = keys.next();
    clothes_num[idx++] = map.get(key);
    
}

int comb_cnt = 1;
while(comb_cnt <= comb_max)
{
    answer += getCombNum(clothes_num, comb_cnt, 1, 0);
    comb_cnt++;
}
일단 옷의 종류를 key로 하여 종류별로 몇 벌의 옷이 있는지 map에 저장한다. 이 때 getOrDefault함수는 아주 유용하게 쓰인다 처음 들어가는 key이면 초기화를 해주고 아닐 경우 해당 값의 1증가한 값을 넣어준다. 필자의 아이디어는 k개의 조합의 수를 구해다주는 함수가 있을 때, 1부터 옷의 모든 종류 수로 k를 늘려가면서 조합의 수를 다 더해주면 된다고 생각했다. 이 함수에 대한 세부 설명은 뒤로 미루고, clothes_num을 선언해 종류별 옷의 개수를 담아준다. 그리고 comb_cnt를 1부터 comb_max로 늘려주면서 getCombNum까지 조합의 수를 다 더해준다.

이제 함수를 보도록하자. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static int getCombNum(int[] arr, int k, int n, int idx)
{
    if(k == 0)
        return n;
    else
    {
        int total = 0; 
        for(int i = idx; i <= arr.length-k; i++)
        {
            total += getCombNum(arr, k-1, n*arr[i], i+1);
        }
        return total;
    }
}
조합의 수를 구해주는 함수이다 arr는 옷의 개수 k는 몇 개의 조합을 원하는지 알려주는 변수이다. n은 현재까지 계산된 조합의 수이며, idx는 arr에서 새로 시작해야하는 index이다. 종료 조건은 k가 0이 될 때이다. 종류개수를 전부 만족했으므로 여태까지 계산한 n을 반환하면 된다. 아닐 경우 조합을 만들어야 한다. total을 0으로 하고, idx부터 length-k까지 n에 arr[i]를 곱해 함수를 재호출한다. 이때 i의 범위가 이해가 잘 안 갈수도 있는데 만약 1,2,3,4,5가 들어간 배열이 있고 2개의 조합을 찾으려고 할 때, 앞에서부터 조합을 만들어간다고 가정하면 1,2,3,4가 가능하다. 여기서 3을 만약 선택했다면 그 다음 조합은 4,5중에 하나를 선택해야한다. 중복없는 모든 조합을 찾기 위한 방법이니 이 참에 잘 공부했으면 좋겠다.

필자는 처음에 이렇게 코드를 짜고 싶지 않았는데 왜냐하면 이렇게 프로그램을 짜는 경우 시간복잡도가 어마무시하게 늘어나기 때문이다. 옷의 종류가 총 n개라고 하고 k개를 선택한다고 하면 함수는 조합 수 만큼 호출되기 때문에 \(O(n^k)\)만큼 호출될 것이다. k의 최대값은 n이므로 결국 \(O(n^n)\)이 된다.

테스트



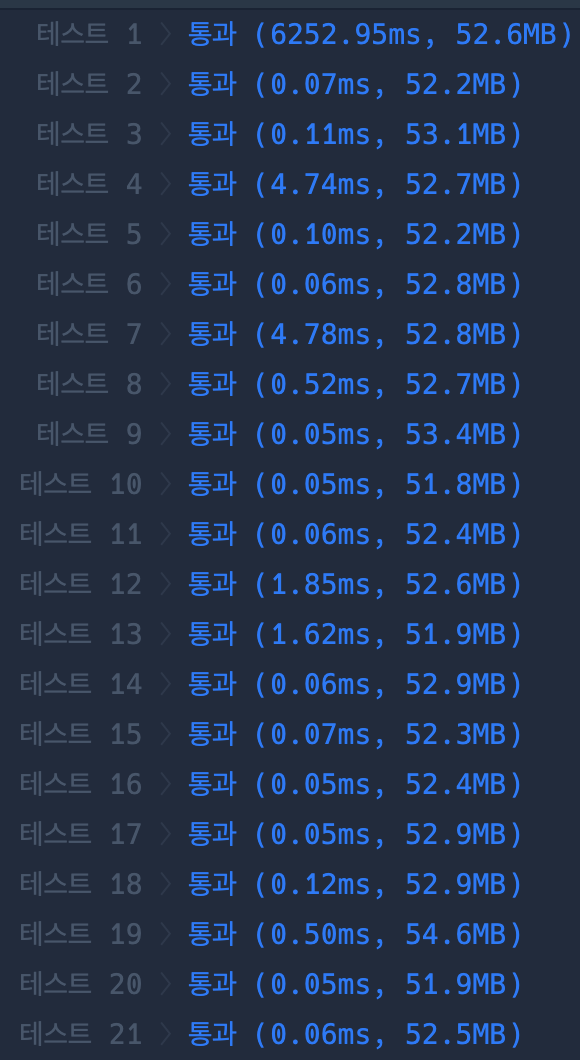
살인적인 시간복잡도를 보고 기겁을 할 수도 있는데, 다행히 통과는 했다. 일부러 1번 케이스를 보여줬는데, 통과는 되었다만 엄청난 시간복잡도를 자랑한다.. 다른 사람의 풀이를 보니 곱할 때 아무것도 선택하지 않은 것도 옵션으로 넣어 \(O(n)\)으로 끝내는 것을 보고 역시 수학을 잘해야 유리하다는 생각이 들었다. 아무튼 풀어냈지만, 수학 공부도 게을리 하지 말아야겠다.