2xn 타일링

문제정의

---

가로 길이가 2이고 세로의 길이가 1인 직사각형 모양의 타일이 있다. 이 타일로 2*n바닥을 덮을 수 있는 경우의 수를 구하는 문제이다.

문제풀이

---

전체 코드는 다음과 같다.

public class Tiling2 {

    //프로그래머스 문제풀이 Level3 2xn 타일링

    public static int[] cache;
    public static void main(String[] args) {
        int n = 4;
        cache = new int[n];
        int answer = ReturnAnswer(n, 0);
        
    }

    public static int ReturnAnswer(int n, int w)
    {
        if(w == n)
            return 1;
        else if(w > n)
            return 0;
        else if(cache[w] != 0)
            return cache[w];
        else
        {
            int res = 0;
            res = ReturnAnswer(n,w+1) % 1000_000_007;
            res += ReturnAnswer(n, w+2) % 1000_000_007;
            cache[w] = res%1000_000_007;
            return cache[w];
        }
    }
    
}

생각해보면 세로길이2를 채울 수 있는 경우의 수는 2가지 밖에 없다. 하나는 세로로 하나의 타일이 쌓인 경우이고, 나머지 하나는 가로로 두개의 타일이 쌓인 경우이다. 첫번째 경우에는 가로로 1증가하고, 두번째 경우는 가로가 2증가한다. 이 두가지 경우를 계속 시도해보는 코드를 짜면 된다.

ReturnAnswer함수를 살펴보자. n은 주어진 가로 길이이고 w는 현재 가로 길이다. 만약 이 가로 길이에 도달하면 1을 반환하고 그렇지 않으면 0을 반환한다. 여기서 연산의 반복을 줄이기 위해 캐시도 사용한다. 만약 해당 길이에 이미 구해놓은 값이 있으면 그 값을 사용한다.

새로 계산해야 하는 경우 길이를 1늘린 것과 2늘린 값을 가져와서 나머지 연산을 한다. 이 둘은 더하는 과정에서도 값이 1,000,000,007을 넘는 경우가 있으므로 캐시에 값을 넣을 때도 나머지 연산을 한 뒤 값을 반환한다.

시간 복잡도는 \(O(log2^n)\)이다.

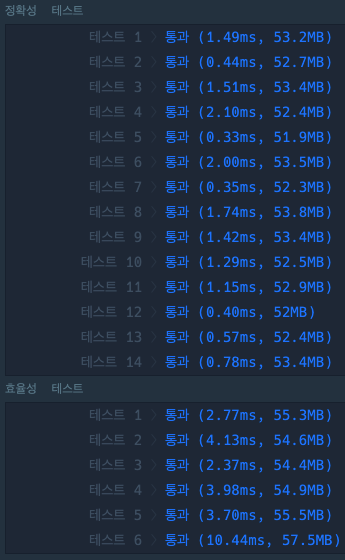
테스트