Rabbit blog

문제정의

0-1 knapsack 문제이다.

문제풀이

이번에는 내 코드와 강사님이 최적화를 거친 코드를 단계로 보며 DP에 대해 정리하려고 한다. 일단 필자의 코드는 아래와 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

N, K = map(int, input().split(" "))

values = []
weights = []

max_dict = {}

for _ in range(N):
    w, v = map(int, input().split(" "))
    values.append(v)
    weights.append(w)

def knapsack(values, weights, n, W):
    if W <= 0 or n == 0:
        return 0
    
    if (n-1, W) in max_dict:
        return max_dict[(n-1, W)]

    res = 0
    if W >= weights[n-1]:
        res =  max(knapsack(values, weights, n-1, W), 
        knapsack(values, weights, n-1, W-weights[n-1]) + values[n-1])
    else:
        res = knapsack(values, weights, n-1, W)

    max_dict[(n-1, W)] = res
    return res
    

print(knapsack(values, weights, N, K))

재귀를 이용한 구현이다. 가용치를 W라하고, n을 넣을 물건의 고유번호라고 생각하면, 이 둘이 0일 때 반환하는 값은 0이다.

계산했던 값을 저장하기 위해 max_dict 딕셔너리를 이용하였다. 여기에 들어가는 키 값은 물건의 고유번호와 가용치가 묶인 튜플이다. 값으로는 최대가치를 반환한다.

이 값이 만약에 존재한다면 계산 해뒀던 값이므로 이 값을 반환한다. 그렇지 않은 경우 값을 새로 계산하여야 한다. 만약 가용치안에 현재 물건이 들어갈 수 있다면, 들어간 경우와 그렇지 않은 경우를 모두 고려하여 값을 계산한다.

가용치안에 물건이 들어갈 수 없다면 없는 경우만 고려하면 된다. 이 때 계산한 값을 딕셔너리에 저장하는 것을 잊지말자!

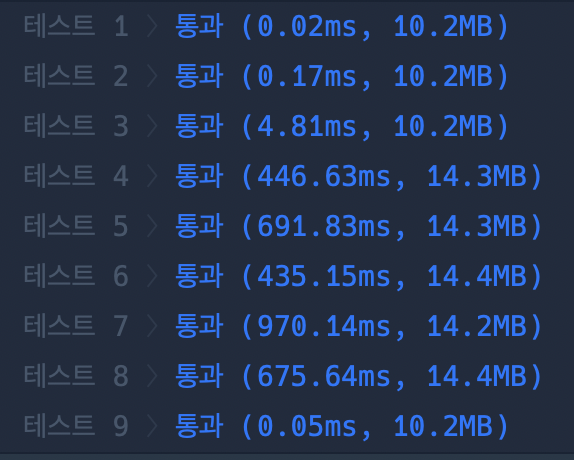
백준에 결과를 돌려보면 다음과 같다.

이제 여기서 최적화를 한 단계씩 해나갈 수 있다. 기존의 Top-down방식을 Bottom-up으로 구성하면 코드는 다음과 같이 변경할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

N, K = map(int, input.split())

W = [0] * (N + 1)
V = [0] * (N + 1)
for i in range(1, N + 1):
    W[i], V[i] = map(int, input.split())

dp = [[0 for _ in range(K+1)] for _ in range(N+1)]

for i in range(1, N+1):
    for w in range(1, K+1):
        if w >= W[i]:
            dp[i][w] = max(dp[i-1][w], dp[i-1][w-W[i]] + V[i])
        else:
            dp[i][w] = dp[i-1][w]


print(dp[N][K]) 

dp라는 2차원 리스트를 만들어서 i번째 물건을 가중치 W에 따라 넣는 경우와 넣지 않는 경우, 넣지 못하는 경우를 전부 기록한다.

위와 비교하여 메모리도 늘고 시간도 늘었다. 실은 이건 재귀에 비하면 느릴 수 있는게 애초에 2차원 배열의 모든 요소를 사용하지 않기 때문에 메모리 낭비가 있기 때문이다. 그리고 표의 모든 요소를 채우기 때문에 시간도 그만큼 오래 걸린다. 하지만 재귀같은 경우 998번이 넘는 호출을 할수가 없기 떄문에 데이터 값이 큰 경우 재귀는 사용하기 어렵기 때문에 이걸 알아놔야 한다.

여기서 보이는 개선 방안은 크게 두가지 이다.

1. 공간의 낭비
2. 표의 모든 요소를 계산할 필요가 없는 것

이 두가지를 최적화 시켜나가려고 한다. 일단 공간적인 면에서 최적화를 시켜보자. 코드를 자세히 보면 점화식을 사용하는 부분에서 i-1번째 줄만 사용하는 것을 볼 수 있다. 그럼 그 이전의 행은 더 이상 쓸 일이 없으므로 이 부분에 대해서 최적화를 하면 다음과 같은 코드로 변경할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

N, K = map(int, input().split())

W = [0] * (N + 1)
V = [0] * (N + 1)
for i in range(1, N + 1):
    W[i], V[i] = map(int, input().split())

dp = [[0 for _ in range(K+1)] for _ in range(2)]

for i in range(1, N+1):
    for w in range(1, K+1):
        if w >= W[i]:
            dp[i%2][w] = max(dp[(i-1)%2][w], dp[(i-1)%2][w-W[i]] + V[i])
        else:
            dp[i%2][w] = dp[(i-1)%2][w]


print(dp[N%2][K]) 

i값에 따라 번갈아 가면서 값을 쓸 수 있도록 하였다.

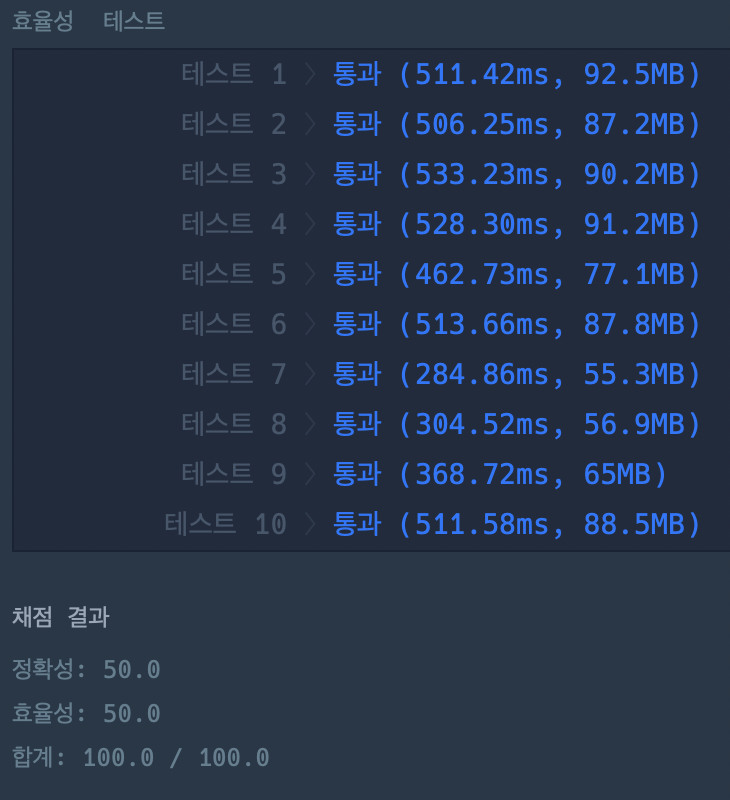
연산 횟수는 다르지 않기 때문에 걸리는 시간은 그대로지만, 메모리 사용량이 크게 준 것을 확인하였다.

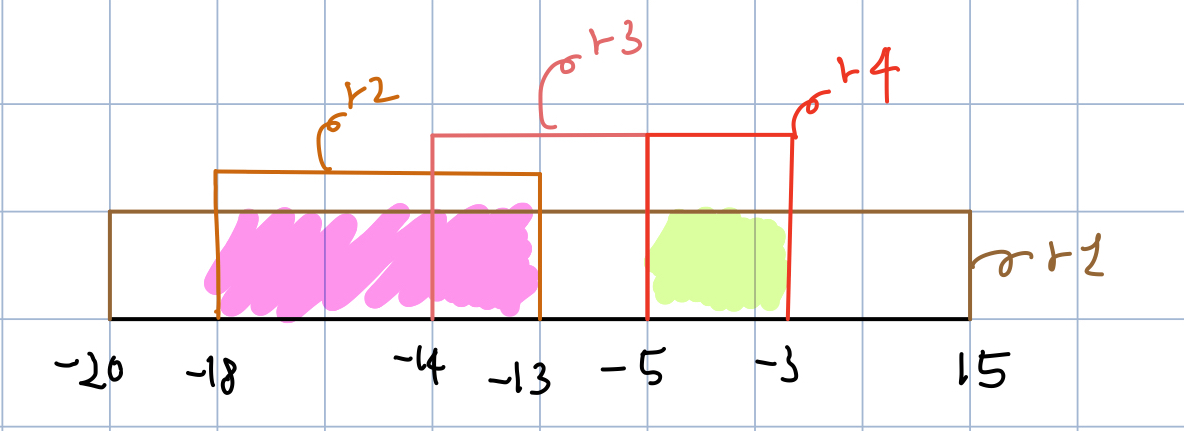
여기서 이제 2번에 대한 최적화를 추가로 할 수 있다. 연산량을 줄이는 것인데, 재귀로 코드를 짰을 때 호출되는 w 값을 계산하여 이를 저장하고 for문에서 이 값들에 대한 계산만 하면 최적화를 할 수 있다.

코드는 아래와 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

N, K = map(int, input().split())

W = [0] * (N + 1)
V = [0] * (N + 1)

for i in range(1, N + 1):
    W[i], V[i] = map(int, input().split())

need_calc = [set() for _ in range(N + 1)]

need_calc[N].add(K)
for i in range(N, -1, -1):
    for w in need_calc[i]:
        if i == 0 or w == 0:
            continue

        if w >= W[i]:
            need_calc[i-1].add(w-W[i])
        need_calc[i-1].add(w)

dp = [[0 for _ in range(K + 1)] for _ in range(2)]
for i in range(1, N + 1):
    for w in need_calc[i]:
        if w >= W[i]:
            dp[i%2][w] = max(dp[(i-1)%2][w], dp[(i-1)%2][w-W[i]] + V[i])
        else:
            dp[i%2][w] = dp[(i-1)%2][w]

print(dp[N%2][K])

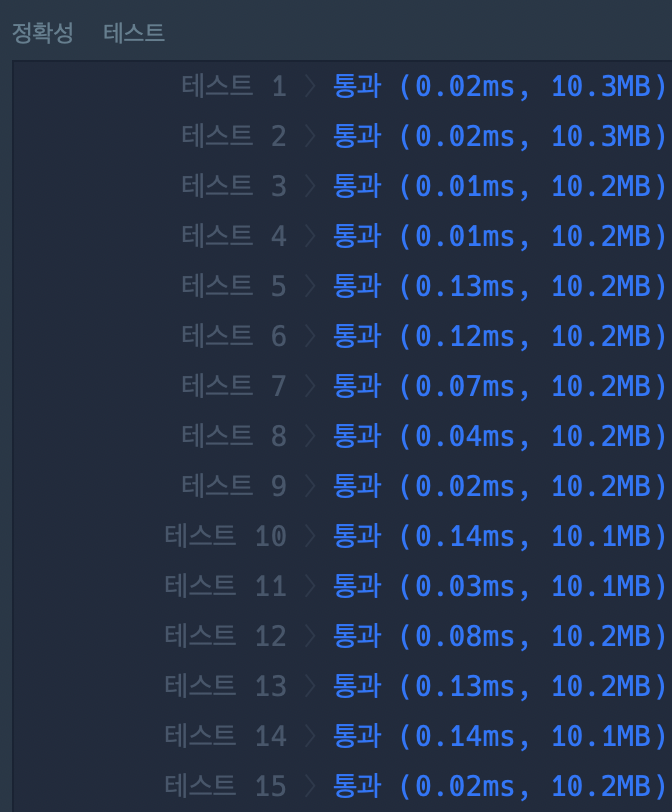
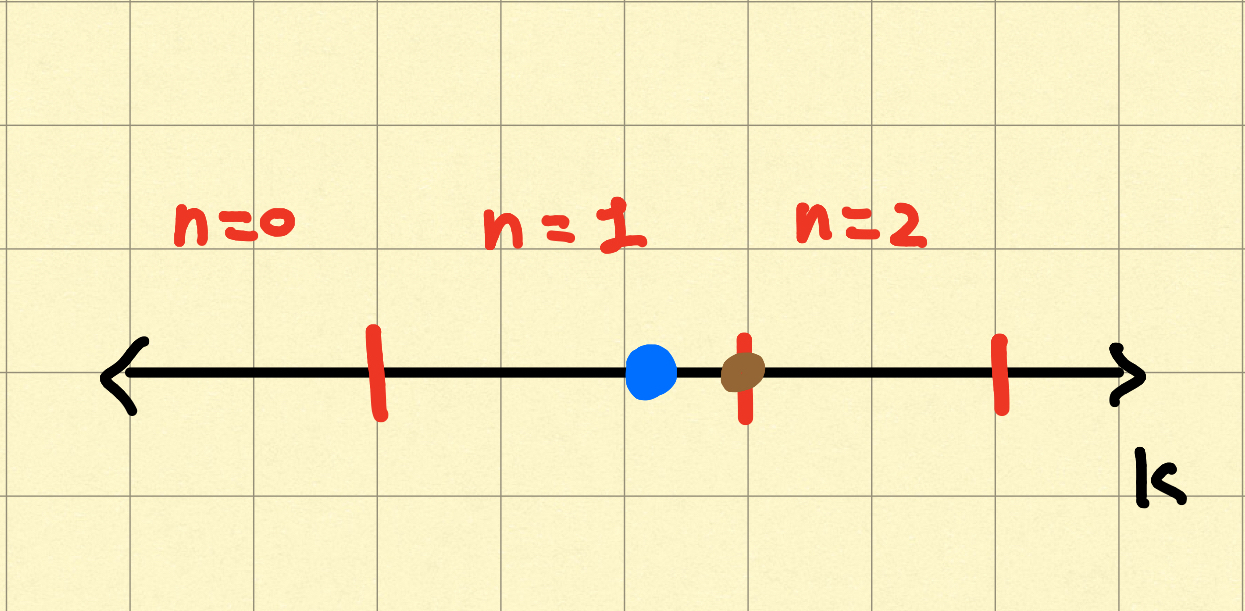
첫번째 for문을 주목하자. 우리는 이미 점화식을 통해 계산해야 하는 w값을 알 수 있다. 그래서 초기에 최종 가용치만을 넣어두고 여기에서 두 경우(선택하는 경우와 하지 않는 경우)로 나누어서 계산에 쓰이는 w값만 need_calc에 넣는다.

오버헤드가 없기 때문에 시간이 재귀보다 단축한 것을 볼 수 있다. 이렇게 최적화 과정에 대해 공부하였는데, 공부를 많이 해야겠다는 생각이 든다. 기죽지 말고 꾸준히 공부해야겠다. ✍️

문제정의

인접한 집을 털지 않으면서 최대한 많은 돈을 도둑질하는 문제이다. 이 때 집은 원형으로 이어져 있다고 가정하기 때문에 첫번째 인덱스와 마지막 인덱스가 이어져있다. 문제 링크

문제풀이

전체 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def solution(money):
    dp1 = [0] * (len(money)-1)
    dp1[0] = money[0]
    dp1[1] = max(money[0], money[1])
    for i in range(2, len(money)-1):
        dp1[i] = max(dp1[i-1], money[i]+dp1[i-2])

    dp2 = [0] * len(money)
    dp2[0] = 0
    dp2[1] = money[1]
    for i in range(2, len(money)):
        dp2[i] = max(dp2[i-1], money[i]+dp2[i-2])
    
    return max(dp1[-1], dp2[-1])

집이 원형으로 이어져있을 때의 조건을 생각하지 못해서 결국 풀이를 봤다. 결론적으로 말하면 첫번째집과 마지막집은 동시에 선택하지 못한다! 그래서 이 경우를 둘로 나눠서 생각한다.

1. 마지막 집을 제외하고 도둑질 할 수 있는 최대 금액을 찾는다.
2. 첫번째 집을 제외하고 도둑질 할 수 있는 최대 금액을 찾는다.
3. 위의 두 값 중에서 큰 값을 반환한다.

이렇게 하면 겹치는 케이스가 존재할 수 있지만 적어도 피하려고 하는 케이스만을 제외하고 나머지 경우의 수를 다 구할 수 있다.

시간 복잡도는 \(O(n)\)이다.

테스트

DP는 너무 어렵다.. 유형중에 제일 해보지 않아서 어색하다. 백준에서 DP문제만 골라 풀어봐야겠다.

문제정의

가로 길이가 2이고 세로의 길이가 1인 직사각형 모양의 타일이 있다. 이 타일로 2*n바닥을 덮을 수 있는 경우의 수를 구하는 문제이다.

문제풀이

전체 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12

def solution(n):
    answer = 0

    fn, fn_1 = 0, 1
    for i in range(n+1):
        fn, fn_1 = fn_1, fn+fn_1
        fn %= 1000000007
        fn_1 %= 1000000007

    return fn % 1000000007

print(solution(4))

시간 복잡도는 \(O(n)\)이다.

테스트

문제정의

베스트 앨범에 곡을 넣는 문제이다. 우선순위는 다음과 같다.

1. 재생 횟수가 가장 많은 장르를 먼저 배치한다.
2. 장르 안에서 재생 횟수가 많은 곡 두개를 넣는다. 곡이 하나라면 하나만 넣는다.
3. 재생 횟수가 동일할 경우 고유번호(인덱스)가 낮은 것을 우선 배치한다.

문제 링크

문제풀이

이번 문제는 기존 내 코드와 파이써닉하게 작성된 코드를 비교하려고 한다. 이건 기존에 혼자 풀이한 코드이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

def solution(genres, plays):
    answer = []
    genre_dict = {}

    for i, genre in enumerate(genres):
        if genre_dict.get(genre) is None:
            genre_dict[genre] = plays[i]
        else:
            v = genre_dict.get(genre)
            genre_dict[genre] = v + plays[i]

    sorted_dict = sorted(genre_dict.items(), key = (lambda x : x[1]), reverse = True)

    for el in sorted_dict:
        song_dict = {}
        for i, genre in enumerate(genres):
            if genre == el[0]:
                song_dict[i] = plays[i]

        sorted_song_dict = sorted(song_dict.items(), key = (lambda x : x[1]), reverse = True)
        for i, item in enumerate(sorted_song_dict):
            if i > 1:
                break
            answer.append(item[0])
            
        
    return answer

genre_dict는 장르별로 총 플레이 횟수를 저장하기 위한 딕셔너리이다. enumerate를 활용하여 장르가 저장되어 있지 않은 경우 새로 등록을 하고, 이미 있는 경우에는 저장된 값에 현재 재생횟수를 추가한다.

genre_dict는 sorted를 활용하여 값을 기준으로 내림차순 정렬을 한다. 이렇게 하면 1번 조건을 만족할 수 있게 된다.

이제 2,3번에 관한 처리를 해야한다. sorted_dict에서 값을 꺼내면서 장르마다 그 장르에 속하는 곡을 찾아낸다. 곡을 찾을 경우 곡의 인덱스를 키로 하고 재생횟수를 값으로 하여 딕셔너리에 추가한다.

이 뒤는 1번과 비슷하다. sorted를 다시 활용하여 값을 기준으로 내림차순 정렬한다(sorted_song_dict).

이제 여기서 2개씩 꺼내서 answer리스트에 추가한다. 들어있는 요소가 한개라면 하나만 넣고 종료한다.

알고리즘은 똑같다. 하지만 파이써닉 하게 작성한 코드를 보면 코드 라인이 확실히 줄어든다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

def solution(genres, plays):
    ht1 = dict()
    ht2 = dict()

    for i, elem in enumerate(zip(genres, plays)):
        g, p = elem
        if g not in ht1:
            ht1[g] = 0
            ht2[g] = []

        ht1[g] += p
        ht2[g].append((i, p))
                    #(g,p)              # -p 내림차순!
    sort_ht1 = sorted(list(ht1.items()), key = lambda x: -x[1])
    
    for g,p in sort_ht1:
        sort_ht2 = sorted(ht2[g], key= lambda x: -x[1])
        answer += list(map(lambda x : x[0], sort_ht2))[:2]

    return answer

1. zip을 통해 기존 인덱스 접근과는 다른 접근 방식을 보여준다.
2. sorted에서 람다함수 부분을 보면 reverse속성이 없고 대신 값에 마이너스를 취한 것을 볼 수 있다. 기능의 차이는 없지만 이렇게 한 경우 코드가 더 간결해 보인다.
3. map과 lambda를 활용하여 곡의 고유번호 2개를 가져온다. 이때 list로 묶에 슬라이싱을 한다.

테스트

통과는 하였지만 파이써닉하게 푸는 것은 아직 더 공부가 필요할 것 같다.

문제정의

이분 탐색을 이용한 수 탐색 문제이다.

문제풀이

전체 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

def binary_search(A, key):
    l = 0
    r = len(A)

    while l < r:
        mid = (l+r) // 2
        if A[mid] == key:
            return 1
        elif A[mid] > key:
            r = mid
        else:
            l = mid+1

    return 0

N = int(input())

A = input().split(" ")

for i, _ in enumerate(A):
    A[i] = int(A[i])

A.sort()

M = int(input())

X = input().split(" ")

for i, _ in enumerate(X):
    print(binary_search(A, int(X[i])))

이분 탐색을 구현하는 문제이다. 입력을 받는 부분을 건너 뛰고 binary_search함수를 보면 된다. 인덱스를 기준으로 이분탐색을 진행한다.

테스트

문제정의

징검다리에서 돌을 빼냈을 때 벌어지는 간격의 최솟값이 가장 큰 것을 구하는 것이다. 문제는 여기에서 볼 수 있다.

문제풀이

이진 탐색을 이용한 문제이다. 유형을 익히면 반가운 문제이지만, 처음에 보면 전혀 감이 안 잡힌다.

전체 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

def solution(distance, rocks, n):
    
    def isFeasable(distance, rocks, n, k):
        cnt = 0
        pos = 0
        total = len(rocks)
        for rock in rocks:
            if rock - pos >= k:
                cnt += 1
                pos = rock

        if total-cnt <= n:
            return True

        return False

    answer = 0
    l = 0
    r = distance
    rocks.sort()
    while l < r:
        mid = (l+r) // 2
        if(isFeasable(distance, rocks, n, mid)):
            answer = mid
            l = mid+1
        else:
            r = mid
            
    return answer

print(solution(25, [2, 14, 11, 21, 17], 2))

여기서 왜 돌을 더 빼도 된다는 의미에 대해 알아보기 위해 isFeasable을 살펴보자

1
2
3
4
5
6
7
8
9
10
11
12
13

def isFeasable(distance, rocks, n, k):
    cnt = 0
    pos = 0
    total = len(rocks)
    for rock in rocks:
        if rock - pos >= k:
            cnt += 1
            pos = rock

    if total-cnt <= n:
        return True

    return False

매개변수로 distance, rocks, n, k를 받는다. cnt는 돌의 개수를 의미하고 pos는 현재 선택한 돌의 위치를 본다. total은 총 돌의 개수를 의미한다.

for 문의 의미는 최솟값 k만큼의 간격에 포함되는 돌들을 세겠다는 의미이다. 프로그래머스에서 나온 예제를 보면 돌이 [2, 11, 14, 17, 21]의 순서로 놓여있다. 가령 k가 6이라면 [11, 17]에 위치한 돌이 선택되고 cnt는 2가 된다. total에서 cnt를 빼면 몇 개의 돌이 빠졌는지 볼 수 있고 이 값이 n보다 같거나 작으면 True를 반환한다.

이하에서 True를 반환하는 이유가 있다. 아래의 그림을 보자.

k값이 증가하면 n값도 증가한다. 최솟값이 증가하니 돌 사이의 간격이 더 넓어져야 하기 때문이다. 여기서 우리는 n을 만족하는 최대를 구하려고 한다. 그러면 l이 증가해야 하는 경우를 살펴보아야 한다. 그림을 보면 n의 값이 요구하는 값보다 작을 때 k가 증가해야 함을 볼 수 있다. 이 이유로 인해 비교 연산자 <=를 사용한 것이다.

테스트

자바로 하다가 파이썬으로 넘어오니까 코드가 훨씬 간결해서 놀랐다. 이제부터라도 열심히 애용하겠다.

문제정의

입국 심사관들이 승객들을 심사하는데 걸리는 가장 최소 시간을 구하는 문제이다. 문제 링크

문제풀이

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

import java.util.*;

public class Immigration {

    //프로그래머스 문제풀이 level3 입국심사
    public static void main(String[] args) {
        int n = 6;
        int[] times = {7, 10};

        Arrays.sort(times);
        System.out.println(BinarySearch(times, n, times[times.length-1]));
    }
    public static long BinarySearch(int[] times, int n, long max)
    {
        long l = 1, r = max * n;
        long mid = 0;
        long ans = Long.MAX_VALUE;
        while(l < r)
        {
            mid = (l+r)/2;
            if(isPassed(times, n, mid))
            {
                ans = Math.min(ans, mid);
                r = mid-1;
            }
            else
                l = mid+1;
        }
        return ans;
    }

    public static boolean isPassed(int[] times, int n, long mid)
    {
        int amount = 0;

        for(int i = 0; i < times.length; i++)
            amount +=  mid / times[i];

        if(amount >= n)
            return true;
        return false;
            
    }
    
}

전체 코드는 다음과 같다.

일단 심사하는데 걸리는 시간을 정렬한다. 이 문제를 해결하기 위한 큰 그림은 이분탐색을 활용하는 것이다. 이분탐색의 mid를 걸리는 최대 시간으로 가정한다. 그리고 이 최대시간을 적용했을 때 모든 승객들을 심사할 수 있는지 검사한다. 만약 모든 승객을 검사할 수 있다면 midr값을 줄이고, 아니라면 mid값을 늘린다.

이분 탐색에서 초기 l값은 1로 r값은 가장 오래 걸리는 심사기간에 n을 곱한다. 그 뒤로는 isPassed함수를 통해 모든 승객을 심할 수 있는지 검사하고 만약 검사할 수 있다면, 정답을 더 작은 쪽으로 업데이트하고 r값을 mid+1로 업데이트한다.

그렇지 않다면 mid값이 더 커져야 한다는 의미이므로 l을 mid+1로 업데이트한다.

isPassed를 검사하는 방법은 들어온 mid값에 대해 심사위원의 시간을 나눠서 검사를 할 수 있는 사람의 수를 전부 더해본다. 만약 이 값이 n을 넘는다면, true를 반환하고, 그렇지 않으면 false를 반환한다.

times의 길이를 m이라 하고, times에서 가장 큰 값을 x라 한다면, 최종 시간복잡도는 \[O(mlognx)\]이다.

테스트

처음 풀이를 틀려서 다른 사람의 풀이를 참고했는데, 이게 전형적인 이분탐색 문제라고 해서 알아보지 못한 내 자신이 원망스러웠다. 학교 수업 때 이러한 유형을 풀어본 적이 있기 때문이다. 보통 엄청 큰 수가 나오고 최소 또는 최대를 구하라는 문제가 이분탐색의 유형에 해당된다고 한다. 앞으로는 잘 기억해두어야 겠다.

문제정의

일반적인 우선순위 큐에서 tail에서도 값이 나올 수 있게 만드는 문제이다. I + (숫자)인 경우 숫자를 삽입하는 것이고 "D 1"인 경우 최댓값을 제거하고, "D -1"이라면 최솟값을 제거한다. 이런 명령어들이 담긴 배열을 전부 수행하였을 때, 큐에 남은 최댓값과 최솟값을 배열로 담아 반환하면 된다. 문제링크

문제풀이

전체 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

import java.util.*;

public class DoublePriorityQueue {

    //프로그래머스 문제풀이 level3 이중 우선순위 큐
    public static PriorityQueue<Integer> big;
    public static PriorityQueue<Integer> small;
    public static HashMap<Integer, Integer> big_map;
    public static HashMap<Integer, Integer> small_map;
    
    public static void main(String[] args) {
        String[] operations = {"I 16", "I -5643", "D -1", "D 1", "D 1", "I 123", "D -1"};

        big = new PriorityQueue<Integer>(Collections.reverseOrder());
        small = new PriorityQueue<Integer>();

        big_map = new HashMap<>();
        small_map = new HashMap<>();


        for(String s : operations)
        {
            if(s.equals("D 1") && !big.isEmpty())
            {
                int big_i = big.peek();
                big_map.put(big_i, big_map.getOrDefault(big_i, 0)+1);
                big.poll();
                
            }
            else if(s.equals("D -1") && !small.isEmpty())
            {
                int small_i = small.peek();
                small_map.put(small_i, small_map.getOrDefault(small_i, 0)+1);
                small.poll();
            }
            else if(s.contains("I"))
            {
                int i = Integer.parseInt(s.substring(1).trim());
                big.add(i);
                small.add(i);
            }
            synchroize();
        }
        if(big.isEmpty())
            System.out.println(0);
        else
            System.out.println(big.peek());

        if(small.isEmpty())
            System.out.println(0);
        else
            System.out.println(small.peek());

    }
    public static void synchroize()
    {
        
        while(big_map.getOrDefault(big.peek(), 0) < small_map.getOrDefault(big.peek(), 0)
        && !big.isEmpty())
        {
            int big_i = big.peek();
            big_map.put(big_i, big_map.getOrDefault(big_i, 0)+1);
            big.poll();
        }
        
        while(big_map.getOrDefault(small.peek(), 0) > small_map.getOrDefault(small.peek(), 0)
        && !small.isEmpty())
        {
            int small_i = small.peek();
            small_map.put(small_i, small_map.getOrDefault(small_i, 0)+1);
            small.poll();
        }
    }
    
}

문제점은 우선순위큐에는 tail이라는 개념이 없는 것이다. 애초에 heap으로 구성이 되어 있으니 최대값만 찾거나 최소값만 찾을 수 있다. 필자는 이를 보완하기 위해 우선순위 큐 두개를 활용하기로 했다.

여기에 추가로 두 개의 맵을 선언하는데 맵의 역할은 각 큐에서 어느 숫자가 몇 번 삭제 되었는지 기록하는 용도이다. 우선순위 큐를 두개를 사용하였지만, 실제로는 하나의 큐로 인식하기 때문에 이 두 큐에서 한쪽만 원소가 삭제되면 안된다. 따라서 이 두 큐를 동기화하기 위해 사용된다.

첫 번째 for문을 보자. 일단 최대값을 제거해야 하는 경우 big에서 하나를 제거하고 맵에 삭제된 횟수를 갱신한다. 최솟값을 제거하는 경우도 동일한 원리로 작동한다.

만약 숫자를 삽입하는 경우라면 두 큐에 모두 삽입한다.

삭제 또는 추가를 마칠 때 마다, 동기화를 해야하는데 필자는 이를 synchronize라는 함수를 통해 구현하였다. 함수 내부를 들여다보면, 두 개의 while문이 나타나는데, 두 while문은 동작하는 방식이 동일하므로 첫번째 while문에 대해서 이야기하겠다.

big큐의 가장 첫번째 원소가 삭제된 횟수가 small에서 삭제된 횟수보다 작다면, 이는 지워야 하는 원소이므로 제거한다. big이 비어있지 않는 한 계속 반복하면 된다. 이를 통해 두 큐를 동기화 할 수 있다.

operation의 크기를 n이라 하였을 때, 최종 시간복잡도는 \(O(nlogn)\)이다. 그거보다 시간복잡도가 높지 않을까 생각하는 분이 계실 수도 있는데, 생각해보면 두 큐에 들어갔다 나오는 횟수를 전부 더하면 \(4nlogn\)이다.

테스트

질문하기를 보니까 조건에 부합하지 않게 짜도 통과되는 경우가 있다고 한다. 이 부분에서 좀 더 신경을 써줬으면 좋겠다.

문제정의

최대한 많은 overlap을 하나로 묶을 때, 나오는 집합의 크기를 구하는 문제이다. 상세한 설명은 아래에 계속하겠다. 문제 링크

문제풀이

전체 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

import java.util.*;

class Section implements Comparable<Section>{
    int s;
    int e;
    public Section(int s, int e){
        super();
        this.s = s;
        this.e = e;
    }
    @Override
    public int compareTo(Section sec){
        return this.s - sec.s;
    }

}


public class SpeedTrap {
    
    //프로그래머스 level3 단속카메라
    public static void main(String[] args) {
        int[][] routes = {
            {-20, 15},
            {-14, -5},
            {-18, -13},
            {-5, -3}
        };

        PriorityQueue<Section> pq = new PriorityQueue<>();

        for(int i = 0; i < routes.length; i++)
            pq.add(new Section(routes[i][0], routes[i][1]));

        int cam_cnt = 0;
        while(!pq.isEmpty())
        {
            int end = pq.peek().e;
            while(!pq.isEmpty() && pq.peek().s <= end)
            {
                end = pq.peek().e < end ? pq.peek().e : end;
                pq.poll();
            }
            cam_cnt++;
        }

        System.out.println(cam_cnt);
    }
}

프로그래머스에서 주어진 구간을 수평선 상에 표시하였다. 최소한의 카메라를 설치해야한다는 것은 최대한 차가 많이 다닐 것 같은 길목에 카메라를 놓아야 한다는 것이다. 그 말은 구간이 최대한 많이 겹치는 쪽에 카메라를 놓으면 된다는 것이다.

이를 구현하기 위해서 Section클래스를 선언하였다. 구간의 처음과 끝을 저장해두며, 정렬을 할 때 구간의 시작점을 기준으로 정렬한다.

우선순위 큐를 선언하여 Section을 집어넣는다. 이 큐에서 하나씩 빼면서 최대한 겹칠 수 있는 구간들을 묶을 것이다. 일단 end를 큐의 첫원소의 도착구간으로 설정한다. 그리고 end보다 출발점이 작은 구간은 무조건 겹치므로 이들을 팝한다. 이 때, 팝한 것들 중에 기존 end보다 작은 종료구간이 있다면 그 값으로 대체한다.

이 반복이 마치면 더 이상 겹치는 구간이 없다는 의미이므로 하나로 묶는 작업이 끝난 것이다. 카메라를 설치한다는 의미로 cam_cnt를 1가한다.

우선순위 큐를 사용하였기 때문에 구간의 개수를 n이라 하였을 때, 최종 시간복잡도는 \(O(nlogn)\)이다.

테스트

학교 수업에서 해봤던 문제라 수월하게 풀 수 있었다. 앞으로 나만의 코테 데이터베이스를 더 쌓아나가야지.

문제정의

SJF(Shortest Job First)를 구현하는 문제이다.

문제풀이

전체 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

import java.util.*;

class Job implements Comparable<Job>{
    int request_time;
    int service_time;
    public Job(int request_time, int service_time)
    {
        super();
        this.request_time = request_time;
        this.service_time = service_time;
    }
    @Override
    public int compareTo(Job j)
    {
        return this.service_time - j.service_time;
    }

}

public class DiskController {

    //프로그래머스 문제풀이 level3 디스크 컨트롤러
    public static void main(String[] args) {
        int[][] jobs = {
            {0, 3},
            {1, 2},
            {500, 6},
            // {0, 7},
            // {0, 3},
        };

        Arrays.sort(jobs, (a,b) -> Integer.compare(a[0], b[0]));

        Queue<Job> prepare_q = new LinkedList<>();
        for(int i = 0; i < jobs.length; i++)
            prepare_q.add(new Job(jobs[i][0], jobs[i][1]));

        PriorityQueue<Job> ready_q = new PriorityQueue<>();


        int time = jobs[0][0];
        int total_t = 0;
        int done = 0;
        
        
        while(done != jobs.length)
        {
            while(!prepare_q.isEmpty() && prepare_q.peek().request_time <= time)
                ready_q.add(prepare_q.poll());
            
            if(!ready_q.isEmpty())
            {
                Job job = ready_q.poll();
                time += job.service_time;
                total_t += time - job.request_time;
                done++;
            }
            else
                time = prepare_q.peek().request_time;
        }        

        System.out.println((int)Math.floor(total_t/done));

    }
    
}

주어진 입력은 요청시간 순대로 들어오지 않으므로 이에 대해 람다식으로 정렬을 해주는 것이 우선이다. 람다식을 이용해 정렬한다.

정렬한 배열을 prepare_q에 전부 넣는다. 실은 여기서 개인의 취향대로 여기서도 우선순위 큐를 활용해도 된다. 이 큐는 처리되길 기다리는 작업들을 모아둔 것이라고 보면 된다.

이제 작업을 순차적으로 처리해야 한다. 초기 time을 첫번째 요청시간으로 초기화한다. total_t는 총 반환시간을 의미하며, done은 종료된 작업의 개수를 뜻한다.

반복은 모든 작업이 완료될 때 까지로 한다. 준비 큐(prepare_q)가 비어있지 않을 때, time보다 작거나 같은 요청시간을 가진 작업들을 모두 빼와 대기 큐(ready_q)에 집어넣는다. 이 때 대기 큐에 하나라도 들어가 있다면, 들어온 것 중에서 가장 작은 서비스시간을 가진 것을 꺼낸다. 그리고 time에는 서비스 시간을 더하고 total_t에 time-(요청 시간)을 더해준다. 그리고 done을 1증가한다. 만약에 대기 큐가 비어있다면 준비큐의 맨 앞의 요청시간을 time으로 갱신한다.

정렬을 사용하였기 때문에 작업의 개수를 n이라 하였을 때, 최종 시간복잡도는 \(O(nlogn)\)이다.

테스트

처음에는 우선순위큐를 이용하지 않고 dfs에서 방문기록을 남겼던 것 처럼, 배열을 정렬하고 방문기록을 활용하여 똑같은 논리로 짰었는데 계속 틀렸다. 어제 몇 시간을 고민하다. 결국 다 지우고 우선순위 큐로 구현하였더니 통과가 되었다. 그 전 코드의 문제점이 뭔지 알았으면 좋았을텐데, 앞으로 공부를 하면서 꼬인 논리를 지금 보다 더 능숙하게 풀어냈으면 좋겠다.